Rotation formalisms in three dimensions
From Wikipedia, the free encyclopedia
(Redirected from Attitude representations)
In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept extends to classical mechanics where rotational (or angular) kinematics is the science of describing with numbers the purely rotational motion of an object. The orientation
of an object at a given instant is described with the same tools, as it
is defined as an imaginary rotation from a reference placement in
space, rather than an actually observed rotation from a previous
placement in space.According to Euler's rotation theorem the general displacement of a rigid body (or three-dimensional coordinate system) with one point fixed is described by a single rotation about some axis. Such a rotation may be uniquely described by a minimum of three parameters. However, for various reasons, there are several ways to represent it. Many of these representations use more than the necessary minimum of three parameters, although each of them still has only three degrees of freedom.
An example where rotation representation is used is in computer vision, where an automated observer needs to track a target. Let's consider a rigid body, with three orthogonal unit vectors fixed to its body (representing the three axes of the object's local coordinate system). The basic problem is to specify the orientation of these three unit vectors, and hence the rigid body, with respect to the observer's coordinate system, regarded as a reference placement in space.
Contents
Formalism alternatives
Rotation matrix
Main article: Rotation matrix
The above mentioned triad of unit vectors is also called a basis. Specifying the coordinates (scalar components)
of this basis in its current (rotated) position, in terms of the
reference (non-rotated) coordinate axes, will completely describe the
rotation. The three unit vectors 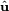 ,
, 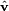 and
and  which form the rotated basis each consist of 3 coordinates, yielding a
total of 9 parameters. These parameters can be written as the elements
of a 3 × 3 matrix
which form the rotated basis each consist of 3 coordinates, yielding a
total of 9 parameters. These parameters can be written as the elements
of a 3 × 3 matrix 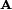 , called a rotation matrix.
Typically, the coordinates of each of these vectors are arranged along a
column of the matrix (however, beware that an alternative definition of
rotation matrix exists and is widely used, where the vectors
coordinates defined above are arranged by rows[1])
, called a rotation matrix.
Typically, the coordinates of each of these vectors are arranged along a
column of the matrix (however, beware that an alternative definition of
rotation matrix exists and is widely used, where the vectors
coordinates defined above are arranged by rows[1])- A is a real, orthogonal matrix, hence each of its rows or columns represents a unit vector.
- The eigenvalues of A are
-
- where i is the standard imaginary unit with the property i2 = −1
- The determinant of A is +1, equivalent to the product of its eigenvalues.
- The trace of A is
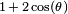 , equivalent to the sum of its eigenvalues.
, equivalent to the sum of its eigenvalues.
 which appears in the eigenvalue expression corresponds to the angle of the Euler axis and angle representation. The eigenvector
corresponding with the eigenvalue of 1 is the accompanying Euler axis,
since the axis is the only (nonzero) vector which remains unchanged by
left-multiplying (rotating) it with the rotation matrix.
which appears in the eigenvalue expression corresponds to the angle of the Euler axis and angle representation. The eigenvector
corresponding with the eigenvalue of 1 is the accompanying Euler axis,
since the axis is the only (nonzero) vector which remains unchanged by
left-multiplying (rotating) it with the rotation matrix.The above properties are equivalent to:
 form a 3D orthonormal basis.
Note that the statements above constitute a total of 6 conditions (the
cross product contains 3), leaving the rotation matrix with just 3
degrees of freedom as required.
form a 3D orthonormal basis.
Note that the statements above constitute a total of 6 conditions (the
cross product contains 3), leaving the rotation matrix with just 3
degrees of freedom as required.Two successive rotations represented by matrices
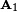 and
and  are easily combined as follows:
are easily combined as follows: 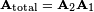 (Note the order, since the vector being rotated is multiplied from the
right). The ease by which vectors can be rotated using a rotation
matrix, as well as the ease of combining successive rotations, make the
rotation matrix a very useful and popular way to represent rotations,
even though it is less concise than other representations.
(Note the order, since the vector being rotated is multiplied from the
right). The ease by which vectors can be rotated using a rotation
matrix, as well as the ease of combining successive rotations, make the
rotation matrix a very useful and popular way to represent rotations,
even though it is less concise than other representations.Euler axis and angle (rotation vector)
Main article: Axis angle
From Euler's rotation theorem
we know that any rotation can be expressed as a single rotation about
some axis. The axis is the unit vector (unique except for sign) which
remains unchanged by the rotation. The magnitude of the angle is also
unique, with its sign being determined by the sign of the rotation axis.The axis can be represented as a three-dimensional unit vector
![\scriptstyle \hat{\mathbf{e}} \;=\; [e_x\ e_y\ e_z]^\mathrm{T}](http://upload.wikimedia.org/math/d/3/c/d3c4369ade559fc4a8a11fe72040f6e8.png) , and the angle by a scalar
, and the angle by a scalar  .
.Since the axis is normalized, it has only two degrees of freedom. The angle adds the third degree of freedom to this rotation representation.
One may wish to express rotation as a rotation vector, a non-normalized three-dimensional vector the direction of which specifies the axis, and the length of which is
 :
:If the rotation angle
 is zero, the axis is not uniquely defined. Combining two successive
rotations, each represented by an Euler axis and angle, is not
straightforward, and in fact does not satisfy the law of vector
addition, which shows that finite rotations are not really vectors at
all. It is best to employ the rotation matrix or quaternion notation,
calculate the product, and then convert back to Euler axis and angle.
is zero, the axis is not uniquely defined. Combining two successive
rotations, each represented by an Euler axis and angle, is not
straightforward, and in fact does not satisfy the law of vector
addition, which shows that finite rotations are not really vectors at
all. It is best to employ the rotation matrix or quaternion notation,
calculate the product, and then convert back to Euler axis and angle.Euler rotations
Main article: Euler angles#Euler rotations
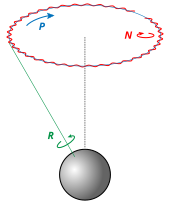
The idea behind Euler rotations is to split the complete rotation of
the coordinate system into three simpler constitutive rotations, called Precession, Nutation, and intrinsic rotation, being each one of them an increment on one of the Euler angles.
Notice that the outer matrix will represent a rotation around one of
the axes of the reference frame, and the inner matrix represents a
rotation around one of the moving frame axis. The middle matrix
represent a rotation around an intermediate axis called line of nodes.Unfortunately, the definition of Euler angles is not unique and in the literature many different conventions are used. These conventions depend on the axes about which the rotations are carried out, and their sequence (since rotations are not commutative).
The convention being used is usually indicated by specifying the axes about which the consecutive rotations (before being composed) take place, referring to them by index (1, 2, 3) or letter (X, Y, Z). The engineering and robotics communities typically use 3-1-3 Euler angles. Notice that after composing the independent rotations, they do not rotate about their axis anymore. The most external matrix rotates the other two, leaving the second rotation matrix over the line of nodes, and the third one in a frame comoving with the body. There are 3×3×3 = 27 possible combinations of three basic rotations but only 3×2×2 = 12 of them can be used for representing arbitrary 3D rotations as Euler angles. These 12 combinations avoid consecutive rotations around the same axis (such as XXY) which would reduce the degrees of freedom that can be represented.
Therefore Euler angles are never expressed in terms of the external frame, or in terms of the co-moving rotated body frame, but in a mixture. Other conventions (e.g., rotation matrix or quaternions) are used to avoid this problem.
Quaternions
Main article: Quaternions and spatial rotation
Quaternions
(Euler symmetric parameters) have proven very useful in representing
rotations due to several advantages above the other representations
mentioned in this article.A quaternion representation of rotation is written as a normalized four-dimensional vector
Inspection shows that the quaternion parametrization obeys the following constraint:
 with
with 
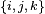 are the hypercomplex numbers satisfying
are the hypercomplex numbers satisfying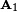 followed by
followed by  , are combined as follows:
, are combined as follows:- More compact than the matrix representation and less susceptible to round-off errors
- The quaternion elements vary continuously over the unit sphere in
 , (denoted by
, (denoted by 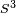 ) as the orientation changes, avoiding discontinuous jumps (inherent to three-dimensional parameterizations)
) as the orientation changes, avoiding discontinuous jumps (inherent to three-dimensional parameterizations) - Expression of the rotation matrix in terms of quaternion parameters involves no trigonometric functions
- It is simple to combine two individual rotations represented as quaternions using a quaternion product
Rodrigues parameters
Main article: Euler–Rodrigues parameters
See also: Rodrigues' rotation formula
Rodrigues parameters can be expressed in terms of Euler axis and angle as follows:Similarly, the Gibbs representation can be expressed as follows:
 , which is the same representation as 180° rotation about (1, 0.0001, 0).)
, which is the same representation as 180° rotation about (1, 0.0001, 0).)Modified Rodrigues parameters (MRPs) can be expressed in terms of Euler axis and angle by:
Cayley–Klein parameters
| This section requires expansion. (September 2013) |
Higher dimensional analogues
Conversion formulae between formalisms
Rotation matrix ↔ Euler angles
The Euler angles can be extracted from the rotation matrix
can be extracted from the rotation matrix 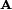 by inspecting the rotation matrix in analytical form.
by inspecting the rotation matrix in analytical form.Using the x-convention, the 3-1-3 Euler angles
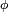 ,
,  and
and  (around the
(around the 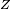 ,
,  and again the
and again the 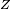 -axis) can be obtained as follows:
-axis) can be obtained as follows: is equivalent to
is equivalent to 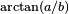 where it also takes into account the quadrant that the point
where it also takes into account the quadrant that the point  is in; see atan2.
is in; see atan2.When implementing the conversion, one has to take into account several situations:[2]
- There are generally two solutions in (−π, π]3 interval. The above formula works only when
 is from the interval [0, π)3.
is from the interval [0, π)3. - For special case
 ,
,  shall be derived from
shall be derived from  .
. - There is infinitely many but countably many solutions outside of interval (−π, π]3.
- Whether all mathematical solutions apply for given application depends on the situation.
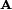 is generated from the Euler angles by multiplying the three matrices generated by rotations about the axes.
is generated from the Euler angles by multiplying the three matrices generated by rotations about the axes. ,
, 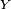 and
and 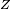 axes with angles
axes with angles 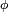 ,
,  and
and  , the individual matrices are as follows:
, the individual matrices are as follows:Rotation matrix ↔ Euler axis/angle
|
|
It has been suggested that Rotation matrix#Conversion from and to axis-angle be merged into this section. (Discuss) Proposed since September 2013. |
 is not a multiple of
is not a multiple of  , the Euler axis
, the Euler axis ![\scriptstyle \hat{\mathbf{e}} \;=\; [e_1\ e_2\ e_3]^\mathrm{T}](http://upload.wikimedia.org/math/e/9/b/e9b3960215a00bfe38d2387576787203.png) and angle
and angle  can be computed from the elements of the rotation matrix
can be computed from the elements of the rotation matrix 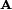 as follows:
as follows:Eigen-decomposition of the rotation matrix yields the eigenvalues 1, and
 . The Euler axis is the eigenvector corresponding to the eigenvalue of 1, and the
. The Euler axis is the eigenvector corresponding to the eigenvalue of 1, and the  can be computed from the remaining eigenvalues.
can be computed from the remaining eigenvalues.The Euler axis can be also found using Singular Value Decomposition since it is the normalized vector spanning the null-space of the matrix
 .
.To convert the other way the rotation matrix corresponding to an Euler axis
![\scriptstyle \hat{\mathbf{e}} \;=\; [e_1\ e_2\ e_3]^\mathrm{T}](http://upload.wikimedia.org/math/e/9/b/e9b3960215a00bfe38d2387576787203.png) and angle
and angle  can be computed according to the Rodrigues' rotation formula (with appropriate modification) as follows:
can be computed according to the Rodrigues' rotation formula (with appropriate modification) as follows: the 3 × 3 identity matrix, and
the 3 × 3 identity matrix, andRotation matrix ↔ quaternion
When computing a quaternion from the rotation matrix there is a sign ambiguity, since and
and 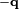 represent the same rotation.
represent the same rotation.One way of computing the quaternion
![\scriptstyle \mathbf{q} \;=\; [q_1\ q_2\ q_3\ q_4]^\mathrm{T}](http://upload.wikimedia.org/math/e/b/6/eb6b13543887188d45953803448ffbf1.png) from the rotation matrix
from the rotation matrix 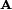 is as follows:
is as follows: .
Numerical inaccuracy can be reduced by avoiding situations in which the
denominator is close to zero. One of the other three methods looks as
follows:[3]
.
Numerical inaccuracy can be reduced by avoiding situations in which the
denominator is close to zero. One of the other three methods looks as
follows:[3]![\scriptstyle \mathbf{q} \;=\; [q_1\ q_2\ q_3\ q_4]^\mathrm{T}](http://upload.wikimedia.org/math/e/b/6/eb6b13543887188d45953803448ffbf1.png) can be computed as follows:
can be computed as follows: the 3 × 3 identity matrix, and
the 3 × 3 identity matrix, andEuler angles ↔ quaternion
Main article: Conversion between quaternions and Euler angles
We will consider the x-convention 3-1-3 Euler Angles for the
following algorithm. The terms of the algorithm depend on the convention
used.We can compute the quaternion
![\scriptstyle \mathbf{q} = [q_1\ q_2\ q_3\ q_4]^\mathrm{T}](http://upload.wikimedia.org/math/c/6/0/c60bc4eaf224dadeda497f4c2a4bb5ac.png) from the Euler angles
from the Euler angles  as follows:
as follows:![\scriptstyle \mathbf{q} = [q_1\ q_2\ q_3\ q_4]^\mathrm{T}](http://upload.wikimedia.org/math/c/6/0/c60bc4eaf224dadeda497f4c2a4bb5ac.png) , the x-convention 3-1-3 Euler angles
, the x-convention 3-1-3 Euler angles  can be computed by
can be computed byEuler axis/angle ↔ quaternion
Given the Euler axis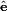 and angle
and angle  , the quaternion
, the quaternion![\scriptstyle \mathbf{q} \;=\; [q_1\ q_2\ q_3\ q_4]^\mathrm{T}](http://upload.wikimedia.org/math/e/b/6/eb6b13543887188d45953803448ffbf1.png) , define
, define ![\scriptstyle \check{\mathbf{q}} \;=\; [q_1\ q_2\ q_3]^\mathrm{T}](http://upload.wikimedia.org/math/7/e/6/7e6304dc5390397c838ce49f1c169898.png) . Then the Euler axis
. Then the Euler axis 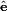 and angle
and angle  can be computed by
can be computed byConversion formulae for derivatives
Rotation matrix ↔ angular velocities
The angular velocity vector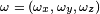 can be extracted from the derivative of the rotation matrix
can be extracted from the derivative of the rotation matrix  by the following relation:
by the following relation:For any vector
 consider
consider  and differentiate it:
and differentiate it: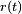 is always equal to the length of
is always equal to the length of  , and hence it does not change with time. Thus, when
, and hence it does not change with time. Thus, when 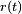 rotates, its tip moves along a circle, and the linear velocity of its
tip is tangential to the circle; i.e., always perpendicular to
rotates, its tip moves along a circle, and the linear velocity of its
tip is tangential to the circle; i.e., always perpendicular to 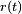 . In this specific case, the relationship between the linear velocity vector and the angular velocity vector is
. In this specific case, the relationship between the linear velocity vector and the angular velocity vector is![\frac{dr}{dt} = \mathbf{\omega}(t)\times r(t) = [\mathbf{\omega}]_\times r(t)](http://upload.wikimedia.org/math/9/7/2/97282d0783aa779d1b83fbdda4f0b6ae.png) (see circular motion and Cross product).
(see circular motion and Cross product).
Quaternion ↔ angular velocities
The angular velocity vector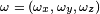 can be obtained from the derivative of the quaternion
can be obtained from the derivative of the quaternion  as follows:[5]
as follows:[5] is the inverse of
is the inverse of  .
.Conversely, the derivative of the quaternion is
Rotors in a geometric algebra
|
|
It has been suggested that this section be merged into Geometric algebra#Rotations. (Discuss) Proposed since September 2013. |
 denotes the outer product. This product of vectors
denotes the outer product. This product of vectors 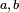 produces two terms: a scalar part from the inner product and a bivector
part from the outer product. This bivector describes the plane
perpendicular to what the cross product of the vectors would return.
produces two terms: a scalar part from the inner product and a bivector
part from the outer product. This bivector describes the plane
perpendicular to what the cross product of the vectors would return.Bivectors in GA have some unusual properties compared to vectors. Under the geometric product, bivectors have negative square: the bivector
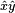 describes the
describes the 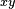 -plane. Its square is
-plane. Its square is  .
Because the unit basis vectors are orthogonal to each other, the
geometric product reduces to the antisymmetric outer product –
.
Because the unit basis vectors are orthogonal to each other, the
geometric product reduces to the antisymmetric outer product –  and
and 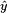 can be swapped freely at the cost of a factor of −1. The square reduces to
can be swapped freely at the cost of a factor of −1. The square reduces to  since the basis vectors themselves square to +1.
since the basis vectors themselves square to +1.This result holds generally for all bivectors, and as a result the bivector plays a role similar to the imaginary unit. Geometric algebra uses bivectors in its analogue to the quaternion, the rotor, given by
 , where
, where  is a unit bivector that describes the plane of rotation. Because
is a unit bivector that describes the plane of rotation. Because  squares to −1, the power series expansion of
squares to −1, the power series expansion of  generates the trigonometric functions. The rotation formula that maps a vector
generates the trigonometric functions. The rotation formula that maps a vector  to a rotated vector
to a rotated vector  is then
is then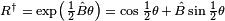 is the reverse of
is the reverse of  (reversing the order of the vectors in
(reversing the order of the vectors in 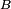 is equivalent to changing its sign).
is equivalent to changing its sign).Example. A rotation about the axis
 can be accomplished by converting
can be accomplished by converting  to its dual bivector,
to its dual bivector,  , where
, where  is the unit volume element, the only trivector (pseudoscalar) in three-dimensional space. The result is
is the unit volume element, the only trivector (pseudoscalar) in three-dimensional space. The result is  . In three-dimensional space, however, it is often simpler to leave the expression for
. In three-dimensional space, however, it is often simpler to leave the expression for  , using the fact that
, using the fact that  commutes with all objects in 3D and also squares to −1. A rotation of the
commutes with all objects in 3D and also squares to −1. A rotation of the  vector in this plane by an angle
vector in this plane by an angle  is then
is then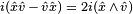 and that
and that  is the reflection of
is the reflection of  about the plane perpendicular to
about the plane perpendicular to  gives a geometric interpretation to the rotation operation: the rotation preserves the components that are parallel to
gives a geometric interpretation to the rotation operation: the rotation preserves the components that are parallel to  and changes only those that are perpendicular. The terms are then computed:
and changes only those that are perpendicular. The terms are then computed: . Such a rotation should map the
. Such a rotation should map the  to
to 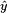 . Indeed, the rotation reduces to
. Indeed, the rotation reduces to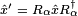 and
and  . These rotors come back out of the exponentials like so:
. These rotors come back out of the exponentials like so: refers to rotation in the original coordinates. Similarly for the
refers to rotation in the original coordinates. Similarly for the  rotation,
rotation,  . Noting that
. Noting that 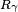 and
and  commute (rotations in the same plane must commute), and the total rotor becomes
commute (rotations in the same plane must commute), and the total rotor becomesWhile rotors in geometric algebra work almost identically to quaternions in three dimensions, the power of this formalism is its generality: this method is appropriate and valid in spaces with any number of dimensions. In 3D, rotations have three degrees of freedom, a degree for each linearly independent plane (bivector) the rotation can take place in. It has been known that pairs of quaternions can be used to generate rotations in 4D, yielding six degrees of freedom, and the geometric algebra approach verifies this result: in 4D, there are six linearly independent bivectors that can be used as the generators of rotations.
![\mathbf{A} =
\left[ {\begin{array}{ccc}
\hat{\mathbf{u}}_x & \hat{\mathbf{v}}_x & \hat{\mathbf{w}}_x \\
\hat{\mathbf{u}}_y & \hat{\mathbf{v}}_y & \hat{\mathbf{w}}_y \\
\hat{\mathbf{u}}_z & \hat{\mathbf{v}}_z & \hat{\mathbf{w}}_z \\
\end{array}} \right]](http://upload.wikimedia.org/math/e/b/8/eb8f2271f313f369169782958925294d.png)
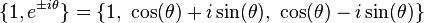



![\hat{\mathbf{q}} = [q_1\ q_2\ q_3\ q_4]^\mathrm{T}](http://upload.wikimedia.org/math/3/d/6/3d6433c59cc56ae4ade81055900b3a97.png)
![\hat{\mathbf{e}} = [e_x\ e_y\ e_z]^\mathrm{T}](http://upload.wikimedia.org/math/c/4/d/c4da2f21e2fd9f76e441b3e6febcbc2d.png)

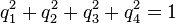

![\tilde{\mathbf{q}}\otimes\mathbf{q} =
\left[ {\begin{array}{rrrr}
q_4 & q_3 & -q_2 & q_1\\
-q_3 & q_4 & q_1 & q_2\\
q_2 & -q_1 & q_4 & q_3\\
-q_1 & -q_2 & -q_3 & q_4
\end{array}} \right]
\left[ {\begin{array}{c}
\tilde{q}_1\\
\tilde{q}_2\\
\tilde{q}_3\\
\tilde{q}_4
\end{array}} \right] =
\left[ {\begin{array}{rrrr}
\tilde{q}_4 & -\tilde{q}_3 & \tilde{q}_2 & \tilde{q}_1\\
\tilde{q}_3 & \tilde{q}_4 & -\tilde{q}_1 & \tilde{q}_2\\
-\tilde{q}_2 & \tilde{q}_1 & \tilde{q}_4 & \tilde{q}_3\\
-\tilde{q}_1 & -\tilde{q}_2 & -\tilde{q}_3 & \tilde{q}_4
\end{array}} \right]
\left[ {\begin{array}{c}
q_1\\
q_2\\
q_3\\
q_4
\end{array}} \right]](http://upload.wikimedia.org/math/5/0/8/5086bc19389b03e85a1e6b1324f8e5f7.png)








![\begin{align}
\mathbf{A}_X &= \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & \cos\phi & \sin\phi\\ 0 & -\sin\phi & \cos\phi \end{array} \right]\\
\mathbf{A}_Y &= \left[\begin{array}{ccc} \cos\theta & 0 & -\sin\theta\\ 0 & 1 & 0\\ \sin\theta & 0 & \cos\theta \end{array} \right]\\
\mathbf{A}_Z &= \left[\begin{array}{ccc} \cos\psi & \sin\psi & 0\\ -\sin\psi & \cos\psi & 0\\ 0 & 0 & 1 \end{array} \right]
\end{align}](http://upload.wikimedia.org/math/8/8/6/8867b40e7d7d69e2db9cba8a7b42d2db.png)
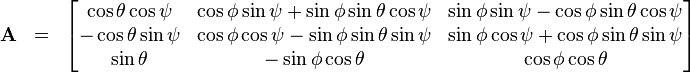
![\begin{align}
\theta &= \arccos\left(\frac{1}{2}[A_{11}+A_{22}+A_{33}-1]\right)\\
e_1 &= \frac{A_{32}-A_{23}}{2\sin\theta}\\
e_2 &= \frac{A_{13}-A_{31}}{2\sin\theta}\\
e_3 &= \frac{A_{21}-A_{12}}{2\sin\theta}
\end{align}](http://upload.wikimedia.org/math/f/4/8/f48d592326f1f53920b8ad155bf809ca.png)
![\mathbf{A} = \mathbf{I}_3\cos\theta + (1-\cos\theta)\hat{\mathbf{e}}\hat{\mathbf{e}}^\mathrm{T} + [\hat{\mathbf{e}}]_{\times} \sin\theta](http://upload.wikimedia.org/math/a/0/9/a096c20be2604d4f5b2b63aa840fa04e.png)
![[\hat{\mathbf{e}}]_{\times} = \left[\begin{array}{ccc} 0 & -e_3 & e_2\\ e_3 & 0 & -e_1\\ -e_2 & e_1 & 0 \end{array} \right]](http://upload.wikimedia.org/math/0/6/d/06d0307d63302624db24f13e16e6acae.png)


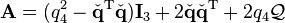
![\check{\mathbf{q}} = \left[\begin{array}{c} q_1\\q_2\\q_3\end{array} \right],\ \ \ \mathbf{\mathcal{Q}} = \left[\begin{array}{ccc} 0 & -q_3 & q_2\\ q_3 & 0 & -q_1\\ -q_2 & q_1 & 0 \end{array} \right]](http://upload.wikimedia.org/math/5/c/e/5ce6b280ee3c7cdc7ddf0194ef15f004.png)
![\mathbf{A} = \left[\begin{array}{ccc}
1 - 2q_2^2 - 2q_3^2 & 2(q_1q_2 - q_3q_4) & 2(q_1q_3 + q_2q_4)\\
2(q_1q_2 + q_3q_4) & 1 - 2q_1^2- 2 q_3^2 & 2(q_2q_3 - q_1q_4)\\
2(q_1q_3 - q_2q_4) & 2(q_1q_4 + q_2q_3) & 1 - 2q_1^2 - 2q_2^2
\end{array} \right]](http://upload.wikimedia.org/math/b/b/9/bb9fe2845d97dd84477f65460beb8a86.png)
![\mathbf{A} = \left[\begin{array}{ccc}
-1 + 2q_1^2 + 2q_4^2 & 2(q_1q_2 - q_3q_4) & 2(q_1q_3 + q_2q_4)\\
2(q_1q_2 + q_3q_4) & -1 + 2q_2^2 + 2q_4^2 & 2(q_2q_3 - q_1q_4)\\
2(q_1q_3 - q_2q_4) & 2(q_1q_4 + q_2q_3) & -1 + 2q_3^2 + 2q_4^2
\end{array} \right]](http://upload.wikimedia.org/math/6/6/0/660f8bebe59018945ab5a7f80c2de211.png)

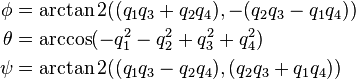
![\mathbf{q} = [q_1\ q_2\ q_3\ q_4]^\mathrm{T}](http://upload.wikimedia.org/math/b/9/d/b9d58ab58ec93ccefbbd2be2ee7d527f.png)
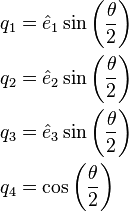

![[\mathbf{\omega}]_\times = \left[\begin{array}{ccc} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{array} \right] = \frac{d\mathbf{A}}{dt}\mathbf{A}^\mathrm{T}](http://upload.wikimedia.org/math/f/1/c/f1cbd0b5f824dce890954b34f3b52471.png)

![\frac{d\mathbf{A}}{dt} \mathbf{A}^\mathrm{T}(t) r(t) = [\mathbf{\omega}]_\times r(t)](http://upload.wikimedia.org/math/8/1/f/81f3be087010efb63c8483a46d43c9d9.png)
![\frac{d\mathbf{A}}{dt} \mathbf{A}^\mathrm{T}(t) = [\mathbf{\omega}]_\times](http://upload.wikimedia.org/math/2/c/5/2c58c189a5a93d7ce28b29fa884404d1.png)
![\left[ {\begin{array}{c}
0 \\
\omega_x \\
\omega_y \\
\omega_z
\end{array}} \right] = 2 \frac{d\mathbf{q}}{dt} \otimes \tilde{\mathbf{q}}](http://upload.wikimedia.org/math/8/1/1/81148dba9112ed3b4e6f834b0d8bebd1.png)
![\frac{d\mathbf{q}}{dt} = \frac{1}{2}\left[ {\begin{array}{c}
0 \\
\omega_x\\
\omega_y\\
\omega_z
\end{array}} \right] \otimes \mathbf{q}](http://upload.wikimedia.org/math/8/c/1/8c1dcda102cfa2b97ca06aa24103f249.png)


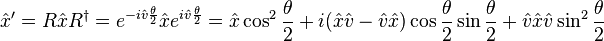

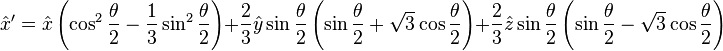


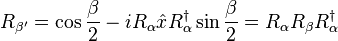
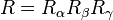



No comments:
Post a Comment